IO Sort Cost Calculation

Nenad Noveljic Leave a Comment

Jonathan Lewis wrote an article about scalar subquery costing. In the course of subsequent experiments we noticed an unusual discrepancy in the IO sort cost for different block sizes. That was also one of the topics in our exchange in the comments of his blog post.

This discrepancy is clearly visible in the sort section of the optimizer trace. See below the excerpts for 8k and 32k database block sizes, respectively:

SORT ressource         Sort statistics
      Sort width:         305 Area size:      268288 Max Area size:    53686272
      Degree:               1
      Blocks to Sort: 196 Row size:     16 Total Rows:         100000
      Initial runs:   2 Merge passes:  1 IO Cost / pass:        108
      Total IO sort cost: 304.000000      Total CPU sort cost: 119218158
      Total Temp space used: 1221000

SORT ressource         Sort statistics
  Sort width:         306 Area size:      268288 Max Area size:    53686272
  Degree:               1
  Blocks to Sort: 49 Row size:     16 Total Rows:         100000
  Initial runs:   2 Merge passes:  1 IO Cost / pass:         74
  Total IO sort cost: 123.000000      Total CPU sort cost: 139966334
  Total Temp space used: 1246000

The only difference in both tests was the block size. Consequently, Blocks to Sort is 4 times higher on the database with the 8k block size. But, the Total IO sort cost is almost three times higher for the 8k database, which doesn’t seem right, because the data volume is exactly the same. I mean a single IO of 32k is usually more efficient than 4 IOs of 8k, but by no means by factor three.

This inconsistency prompted further investigation.

Blocks to Sort

By simple eyeballing I first identified that Total IO sort cost is the sum of two other values exposed in the sort section in the optimizer trace: Blocks to Sort and IO Cost / pass:

(1)   \begin{equation*} Total\ IO\ sort\ cost = Blocks\ to\ Sort + IO\ Cost / pass \end{equation*}

Blocks to Sort is the fixed part of the cost calculation. Therefore, it’s the main contributor to the relatively large difference between the cost calculations for different block sizes.

A more challenging part is to figure out the IO Cost / pass calculation, the other summand in the equation 1.

IO Cost / pass

There isn’t a simple way for cracking the formula for IO Cost / pass based on the system statistics, block sizes etc. So I first had to identify Oracle functions participating in the calculation and then deduce the formula by observing their inputs, outputs and values stored in the registers.

This technique almost always yields a result. On the downside, it’s very time consuming. First, you have to work out the numbers and the arithmetic operations. But then, to interpret this calculation, you need to know where these operands came from, which can recursively create additional layers of investigation.

However, the heuristics based on the general optimizer knowledge can dramatically reduce the research time.

Fortunately, Jonathan had correctly assumed that the calculation depends on the system statistics seek time (IOSEEKTIM) and transfer rate (IOTFRSPEED), which had been set to their default values 10ms and 4k, respectively. So, whenever I observed those numbers somewhere in the registers I reasonably assumed that they had came from the system statistics mentioned. After that, I had to rerun the experiment with changed values to see if the deduced formula still holds.

But first of all, I had to identify the entry point, i.e. a higher level Oracle function involved in the cost calculation.

kkeSortCosts

I did that by enriching trace with call stacks, a troubleshooting technique, which I had described in a previous blog post. Basically, I’m using DTrace for capturing the call stack whenever a string of interest gets written into the trace file:

sudo -u root /usr/sbin/dtrace -p 6178 -s call_stack_trace.d '"Total"'

SORT ressource         Sort statistics
  Sort width:         306 Area size:      268288 Max Area size:    53686272
  Degree:               1
  Blocks to Sort: 49 Row size:     16 Total Rows:         100000
  Initial runs:   2 Merge pas
libc.so.1`__write+0xa
a.out`sdbgrfuwf_write_file+0x42
a.out`sdbgrfwf_write_file+0x3a
a.out`dbgtfdFileWrite+0x210
a.out`dbgtfdFileAccessCbk+0x177
a.out`dbgtfWriteRec+0x585
a.out`dbgtRecVAWriteDisk+0xaa
a.out`dbgtTrcVaList_int+0xa96
a.out`dbgtTrc_int+0xa6
a.out`kkeSortCosts+0x2287
a.out`kkesrcCard+0x63
a.out`kkoqbc+0x36eb
a.out`apakkoqb+0xa1
a.out`apaqbdDescendents+0x20e
a.out`apadrv+0xae5
a.out`opitca+0x9ca
a.out`kksFullTypeCheck+0x4c
oracle`rpiswu2+0x20c
a.out`kksLoadChild+0x29f6
a.out`kxsGetRuntimeLock+0x79d

As you can see, the function kkeSortCosts was the one which produced the trace entries, so I assumed it orchestrates the whole sort cost calculation.

I confirmed that by tracing function calls made by kkeSortCosts. kkesIOScaleFactor is one of such functions, for which I captured a couple of call stacks:

dtrace -q -n 'pid$target::kkesIOScaleFactor:entry{ ustack(); }' -p 28898

a.out`kkesIOScaleFactor
a.out`kkesScaleIO+0xac
a.out`kkeTbScanIOCost+0x24
...
a.out`kkesIOScaleFactor
a.out`kkesScaleIO+0xac
a.out`kkeSortCosts+0xdec
...

As you can see, there are two different cases where the functions kkesIOScaleFactor and kkesScaleIO are called. One is the table scan cost calculation (kkeTbScanIOCost). The other is the sort cost calculation (kkeSortCosts).

Obviously, both kkesScaleIO and kkesIOScaleFactor are generic functions participating in IO cost calculation; as such, they are undoubtedly worth a more detailed examination.

kkesScaleIO

I set up a breakpoint on the exit from kkesScaleIO to record the return values which are passed through the XMM0 register.

break kkesScaleIO_RETURN_ADDRESS
commands 1
p $xmm0
backtrace 3
continue
end

Below are the outputs for 8k and 32k, respectively:

$3 = {v4_float = {0, 3.171875, 0, 0}, v2_double = {54, 0}, v16_int8 = {0, 0, 0, 0, 0, 0, 75, 64, 0, 0, 0, 0, 0, 0, 0, 0}, v8_int16 = {0, 
    0, 0, 16459, 0, 0, 0, 0}, v4_int32 = {0, 1078657024, 0, 0}, v2_int64 = {4632796641680687104, 0}, uint128 = 4632796641680687104}
#0  0x00000000104e5dc3 in kkesScaleIO ()
#1  0x000000000a4e5dbc in kkeSortCosts ()
#2  0x0000000010550133 in kkesrcCard ()
$6 = {v4_float = {0, 3.0390625, 0, 0}, v2_double = {37, 0}, v16_int8 = {0, 0, 0, 0, 0, -128, 66, 64, 0, 0, 0, 0, 0, 0, 0, 0}, v8_int16 = {
    0, 0, -32768, 16450, 0, 0, 0, 0}, v4_int32 = {0, 1078099968, 0, 0}, v2_int64 = {4630404104378646528, 0}, 
  uint128 = 4630404104378646528}
#0  0x00000000104e5dc3 in kkesScaleIO ()
#1  0x000000000a4e5dbc in kkeSortCosts ()
#2  0x0000000010550133 in kkesrcCard ()

By the way, I also included backtrace, just to make sure that the output observed is for the sort cost calculation (as opposed to the tablescan cost calculation).

Subsequently, I compared the return values 54 and 37 with the numbers in the optimizer trace. It was easy to establish the following relationship:

(2)   \begin{equation*} IO\ Cost \ pass = 2 \cdot scaled\ io\ cost \end{equation*}

where:

  • scaled io cost is returned by the function kkesScaleIO,
  • IO Cost / pass is the value recorded in the optimizer trace.

Consequently, the equation Total IO sort cost can be expressed as a function of scaled io cost by combining the equations 1 and 2:

(3)   \begin{equation*} Total\ IO\ sort\ cost = Blocks\ to\ Sort + 2 \cdot scaled\ io\ cost \end{equation*}

Further, by stepping through the function and observing the register values I managed to puzzle out how the return value gets calculated:

(4)   \begin{equation*} \begin{split} \cancel { scaled\ io\ cost = \frac{Blocks\ to\ Sort + 1}{io\ scale\ factor} + 1 } \\ \\ scaled\ io\ cost = \Bigg \lfloor \frac{Blocks\ to\ Sort + 1}{io\ scale\ factor} \Bigg \rfloor + 1 \end{split} \end{equation*}

where io scale factor is the return value of the function kkesIOScaleFactor.

Both +1 in the equation 4 are just the safeguards against the multiplication/division by zero; boundary conditions, which would lead the whole calculation astray.

Knowing Blocks to Sort from the optimizer trace and scaled io cost from the gdb trace, I calculated the values for io scale factor and concluded following: the lower the block size, the higher the io scale factor.

In other words, scaled io cost is Blocks to Sort “softened” by dividing it with io scale factor which is higher for smaller block sizes. Simply put, it’s this division that prevents an incorrect cost explosion for a large number of smaller blocks.

io scale factor calculation in kkesIOScaleFactor is the last bit to resolve.

kkesIOScaleFactor

I observed input and output values for the function. The first argument is passed in the EDI register, the output value is stored in the XMM0 register.

break kkesIOScaleFactor
commands 1
p $edi
continue
end
break kkesIOScaleFactor_RETURN_ADDRESS
commands 2
p $xmm0
backtrace 3
continue
end

Find below the results for 8k and 32k, respectively:

Thread 2 hit Breakpoint 1, 0x00000000104e4bc0 in kkesIOScaleFactor ()
$19 = 8

Thread 2 hit Breakpoint 2, 0x00000000104e4f7e in kkesIOScaleFactor ()
$20 = {v4_float = {-3.6487575e-21, 2.21153831, 0, 0}, v2_double = {3.6923076923076925, 0}, v16_int8 = {-98, -40, -119, -99, -40, -119, 
    13, 64, 0, 0, 0, 0, 0, 0, 0, 0}, v8_int16 = {-10082, -25207, -30248, 16397, 0, 0, 0, 0}, v4_int32 = {-1651910498, 1074629080, 0, 0}, 
  v2_int64 = {4615496756573624478, 0}, uint128 = 4615496756573624478}
#0  0x00000000104e4f7e in kkesIOScaleFactor ()
#1  0x00000000104e5cfc in kkesScaleIO ()
#2  0x000000000a4e5dbc in kkeSortCosts ()
Thread 2 hit Breakpoint 1, 0x00000000104e4bc0 in kkesIOScaleFactor ()
$5 = 2

Thread 2 hit Breakpoint 2, 0x00000000104e4f7e in kkesIOScaleFactor ()
$6 = {v4_float = {8.48740821e+32, 1.92307687, 0, 0}, v2_double = {1.3846153846153846, 0}, v16_int8 = {118, 98, 39, 118, 98, 39, -10, 63, 
    0, 0, 0, 0, 0, 0, 0, 0}, v8_int16 = {25206, 30247, 10082, 16374, 0, 0, 0, 0}, v4_int32 = {1982292598, 1073096546, 0, 0}, v2_int64 = {
    4608914572502852214, 0}, uint128 = 4608914572502852214}
#0  0x00000000104e4f7e in kkesIOScaleFactor ()
#1  0x00000000104e5cfc in kkesScaleIO ()
#2  0x000000000a4e5dbc in kkeSortCosts ()

The input value, let’s call it c, is 8 for 8k and 2 for 32k. So, I deduced the following formula for c:

(5)   \begin{equation*} c = \frac{64}{block\ size\ kb} \end{equation*}

where block size kb is the database block size in kbytes.

Further, by stepping through the function and observing the register values, I deduced the formula for the io scale factor.

(6)   \begin{equation*} io\ scale\ factor = c \cdot \frac{ IOSEEKTIM + \frac{block\ size\ kb}{IOTFRSPEED\ KB} }{ IOSEEKTIM + \frac{64}{IOTFRSPEED\ KB}} \end{equation*}

where:

  • IOSEEKTIM is the system statistic seek time in ms,
  • IOTFRSPEED KB is the system statistic (IOTFRSPEED) expressed in kbytes.

Or after combining the equations 5 and 6:

(7)   \begin{equation*} io\ scale\ factor = \frac{64}{block\ size\ kb} \cdot \frac{ IOSEEKTIM + \frac{block\ size\ kb}{IOTFRSPEED\ KB} }{ IOSEEKTIM + \frac{64}{IOTFRSPEED\ KB}} \end{equation*}

Total IO sort cost formula

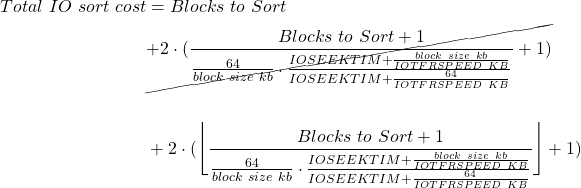
Finally, Total IO sort cost formula can be derived by combining the equations 3, 4 and 7:

(8)   \begin{equation*} \begin{split} Total\ IO\ sort\ cost &= Blocks\ to\ Sort \\ & \cancel {+ 2 \cdot ( \frac{Blocks\ to\ Sort + 1}{\frac{64}{block\ size\ kb} \cdot \frac{ IOSEEKTIM + \frac{block\ size\ kb}{IOTFRSPEED\ KB} }{ IOSEEKTIM + \frac{64}{IOTFRSPEED\ KB}}} + 1 )} \\ \\ &+ 2 \cdot ( \Bigg \lfloor \frac{Blocks\ to\ Sort + 1}{\frac{64}{block\ size\ kb} \cdot \frac{ IOSEEKTIM + \frac{block\ size\ kb}{IOTFRSPEED\ KB} }{ IOSEEKTIM + \frac{64}{IOTFRSPEED\ KB}}} \Bigg \rfloor + 1 ) \end{split} \end{equation*}

Simulator

Also, I wrote a PL/SQL anonymous block that simulates the optimizer calculation in order to verify my assumptions in the course of this research. The only input to the simulator is :blocks_to_sort, whose value is taken from the optimizer trace. All other parameters are dynamically retrieved.

I enclosed it below for those who’d like to experiment further:

set serveroutput on size 1000000

variable blocks_to_sort number
begin 
  :blocks_to_sort := 196 ;
--  :blocks_to_sort := 49 ;
end;
/

declare
  p_blocks_to_sort integer := :blocks_to_sort ;
  
  l_ioseektim sys.aux_stats$.pval1%type ;
  l_iotfrspeed sys.aux_stats$.pval1%type ;
  l_db_block_size integer ;
  l_io_scale_factor number ;
  l_io_cost_per_pass number ;
  l_total_io_sort_cost number ;
begin
  select pval1 into l_ioseektim from sys.aux_stats$ where pname = 'IOSEEKTIM' ;
  select pval1 into l_iotfrspeed from sys.aux_stats$ 
    where pname = 'IOTFRSPEED' 
  ;
  select value into l_db_block_size from v$parameter 
    where name = 'db_block_size' 
  ;

  l_io_scale_factor := 
    ( l_ioseektim + l_db_block_size / l_iotfrspeed  ) * 
    ( 65536 / l_db_block_size ) / ( l_ioseektim + 65536 / l_iotfrspeed  ) 
  ;
  dbms_output.put_line('io scale factor: ' || round(l_io_scale_factor,2) ) ;
  
  l_io_cost_per_pass 
    := 2 * ( ( p_blocks_to_sort + 1 ) / l_io_scale_factor + 1 )  ;
  dbms_output.put_line('IO Cost / pass: ' || floor(l_io_cost_per_pass ) ) ;
  
  l_total_io_sort_cost := p_blocks_to_sort + l_io_cost_per_pass ;
  dbms_output.put_line(
    'Total IO sort cost: ' || floor(l_total_io_sort_cost) ) ;
end ;
/

The computed values for 8k and 32k, respectively, perfectly match the numbers from the optimizer trace:

io scale factor: 3.69
IO Cost / pass: 108
Total IO sort cost: 304
io scale factor: 1.38
IO Cost / pass: 74
Total IO sort cost: 123

Conclusion

In conclusion, the smaller the database block size, the higher the Total IO sort cost. That’s a consequence of Blocks to Sort being a main contributor to the cost.

The other summand in the equation is the value proportional to scaled io cost, the number of blocks divided by the scaling factor. The scaling factor is higher for a smaller block size, i.e. larger number of blocks. This computation, therefore, prevents a cost explosion for the databases with smaller block size.

The same IO cost calculation is performed in other scenarios too, like table scans. So, the insights gained and the methodology used in this research can be used for generally understanding the IO cost calculations.

Updates on October 8, 2020

io_scale_factor

floor on the fraction was missing in the formula for io_scale_factor. This became apparent when I tried to apply it to Jonathan Lewis’ model for investigating an index FFS cost anomaly.

Interpreting formulas

I also wrote a sequel of this article where I interpreted the formulas above.

Thanks for sharing

Nenad Noveljic

More Posts Twitter LinkedIn

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.