The cost calculation might be wrong for an OUTER JOIN executing a correlated scalar subquery. I’ve observed this problem on the Oracle database releases 12.2 and 18.5.

I’ll be using the following tables to show that:

create table t_100k ( ndv_50k integer, ndv_30 integer ) ;
create table t_10k ( ndv_10k integer ) ;
create table t_1k ( ndv_1k  integer ) ;

insert into t_100k
  select 
	mod(level,50000),
	mod(level,30)
    from dual
    connect by level <= 1e5;

insert into t_10k
  select level
    from dual
    connect by level <= 1e4;

insert into t_1k
  select level
    from dual
    connect by level <= 1e3;
    
create index ix_t10k_1 on t_10k(ndv_10k) ;

begin
  dbms_stats.gather_table_stats ( null, 't_100k') ;
  dbms_stats.gather_table_stats ( null, 't_10k' , cascade => true ) ;
  dbms_stats.gather_table_stats ( null, 't_1k') ;
end ;
/

Cost calculation

First, let’s consider the following query:

explain plan for
select /*+ gather_plan_statistics */ distinct 
  t_100k.ndv_30,
  ( select count(*) from t_1k where t_1k.ndv_1k = t_100k.ndv_50k  )  
  from t_100k    
;

set linesize 200
set pagesize 100
select * from table(dbms_xplan.display_cursor(format => 'BASIC LAST +iostats +rows +cost')) ;

-------------------------------------------------------------------------------------------------------------
| Id  | Operation          | Name   | Starts | E-Rows | Cost (%CPU)| A-Rows |   A-Time   | Buffers | Reads  |
-------------------------------------------------------------------------------------------------------------
|   0 | SELECT STATEMENT   |        |      1 |        |   267K(100)|     60 |00:00:03.79 |     198K|     49 |
|   1 |  SORT AGGREGATE    |        |  98976 |      1 |            |  98976 |00:00:03.63 |     197K|      2 |
|*  2 |   TABLE ACCESS FULL| T_1K   |  98976 |      1 |     3   (0)|   1356 |00:00:03.52 |     197K|      2 |
|   3 |  HASH UNIQUE       |        |      1 |     30 |   267K  (1)|     60 |00:00:03.79 |     198K|     49 |
|   4 |   TABLE ACCESS FULL| T_100K |      1 |    100K|    26   (0)|    100K|00:00:00.02 |      49 |     47 |
-------------------------------------------------------------------------------------------------------------

Predicate Information (identified by operation id):
---------------------------------------------------

   2 - filter("T_1K"."NDV_1K"=:B1)

The subquery, which selects from T_1K, returns a scalar value for each row in T_100K.

The query cost, therefore, consists of the following parts: main query block cost (T_100K full table scan in this case), sort operation (because of DISTINCT) and the total cost of the subquery execution.

Let’s focus on the last part for the moment: the total cost of the subquery execution.

If the subquery had been executed for each T_100K row, the total subquery cost would have been the product of the T_100K cardinality and the T_1K full table scan (FTS) cost, which is 300K. But the optimizer came up with a lower number: 267K. This lower cost is a consequence of the scalar subquery result caching. In other words, the optimizer caches the fetched values to reduce the number of subquery executions.

Jonathan Lewis described this cost calculation in [Lewis 2019].

Filling the cache

The scalar subquery cache can store up to 10922 integer values. The cost of initially filling the cache is, therefore:

(1) $\begin{equation*} filling\_cost = cache\_size \cdot single\_subq\_exec\_cost = 10922 \cdot 3 = 32766 \end{equation*}$

where

cache_size is the maximum number of elements in the cache
subq_single_exec_cost is the cost of the single subquery execution.

Cache misses

There will inevitably be some cache misses if all of the results don’t fit into the cache. This will happen when the number of distinct values (NDV) of the outer table join column is greater than the cache size.

The cost of refilling the cache contributes to the total cost. It depends on the probability of a cache miss, which can be calculated as follows:

(2) $\begin{equation*} p = 1 - \frac{cache\_size}{NDV} = 1 - \frac{10922}{50000} = 0.78156 \end{equation*}$

where NDV is the number of distinct values of the outer table join column.

The following formula calculates the total cost of the cache misses:

(3) $\begin{equation*} \begin{split} misses\_cost &= card(main\_qb) \cdot p \cdot subq\_single\_exec\_cost \\ &= card(main\_qb) \cdot ( 1 - \frac{cache\_size}{NDV} ) \cdot subq\_single\_exec\_cost \end{split} \end{equation*}$

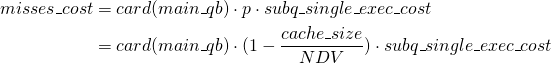
where card(main_qb) is the cardinality of the rows returned by the main query block which is driving the subquery execution.

In our case :

(4) $\begin{equation*} card(main\_qb) = card(t\_100k) \end{equation*}$

(5) $\begin{equation*} NDV = NDV(t\_100k.ndv\_50k ) \end{equation*}$

(6) $\begin{equation*} \begin{split} misses\_cost &= card(t\_100k) \cdot ( 1 - \frac{cache\_size}{NDV(t\_100k.ndv\_50k )} ) \\ &\cdot subq\_single\_exec\_cost \\ &= 100000 \cdot ( 1 - \frac{10922}{50000}) \cdot 3 = 234468 \end{split} \end{equation*}$

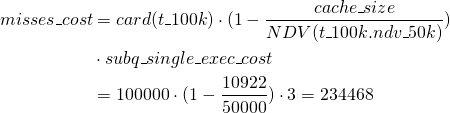
It’s worth noting that the cache misses cost is proportional to the T_100K cardinality.

The total subquery cost is:

(7) $\begin{equation*} total\_subq\_cost = filling\_cost + misses\_cost = 234468 + 32767 = 267234 \end{equation*}$

In this example, the total query cost mainly consists of the total subquery cost, because the overhead of HASH UNIQUE and T100_K FTS is negligible.

Outer join

Next, let’s expand the original query with an OUTER JOIN:


select /*+ gather_plan_statistics */ distinct 
  t_100k.ndv_30,
  ( select count(*) from t_1k where t_1k.ndv_1k = t_100k.ndv_50k )  
  from t_100k, t_10k
  where t_10k.ndv_10k(+) = t_100k.ndv_50k
;

Like in the first query, the subquery will be invoked 100000 times for 50000 different T_100K.NDV_50K values, so the total subquery cost should remain the same. In addition, there is a T_10K retrieval cost and an OUTER JOIN cost, but both of them are negligible. Consequently, the total cost should be just a little higher than the cost of the previous query without the OUTER JOIN.

But, surprisingly, the cost slumped instead of slightly increased:


--------------------------------------------------------------------------------------------------------------------
| Id  | Operation              | Name      | Starts | E-Rows | Cost (%CPU)| A-Rows |   A-Time   | Buffers | Reads  |
--------------------------------------------------------------------------------------------------------------------
|   0 | SELECT STATEMENT       |           |      1 |        | 30069 (100)|     60 |00:00:03.96 |     198K|     57 |
|   1 |  SORT AGGREGATE        |           |  98976 |      1 |            |  98976 |00:00:03.77 |     197K|      2 |
|*  2 |   TABLE ACCESS FULL    | T_1K      |  98976 |      1 |     3   (0)|   1356 |00:00:03.66 |     197K|      2 |
|   3 |  HASH UNIQUE           |           |      1 |     30 | 30069   (1)|     60 |00:00:03.96 |     198K|     57 |
|*  4 |   HASH JOIN RIGHT OUTER|           |      1 |    100K|    32   (4)|    100K|00:00:00.08 |      61 |     55 |
|   5 |    INDEX FAST FULL SCAN| IX_T10K_1 |      1 |  10000 |     5   (0)|  10000 |00:00:00.01 |      12 |      8 |
|   6 |    TABLE ACCESS FULL   | T_100K    |      1 |    100K|    26   (0)|    100K|00:00:00.01 |      49 |     47 |
--------------------------------------------------------------------------------------------------------------------

Predicate Information (identified by operation id):
---------------------------------------------------

   2 - filter("T_1K"."NDV_1K"=:B1)
   4 - access("T_10K"."NDV_10K"="T_100K"."NDV_50K")

By observing the cardinalities and costs we can deduce how the optimizer calculated the total cost. We can see, for example, that the total subquery cost is a little higher than

(8) $\begin{equation*} subq\_single\_exec\_cost \cdot card(T\_10K) = 3 \cdot 10000 = 30000 \end{equation*}$

So, the optimizer, apparently, used T_10K instead of T_100K cardinality to calculate the total subquery cost.

In other words, it operated under the wrong assumption:

(9) $\begin{equation*} card(rowset) = card(T\_100K) = card(T\_10K) \end{equation*}$

But, this symmetry is only valid for the inner join if the join columns are unique. Therefore, the total cost will be massively underestimated when card(inner_table) is much less than card(outer_table). By the way, this problem appears only when there’s a HASH UNIQUE operation on the driving query block row set.

Summary

If an OUTER JOIN is driving the execution of a correlated scalar subquery in the SELECT DISTINCT clause, the optimizer will incorrectly use the cardinality of the inner table for calculating the total cost of the subquery. Larger the gap between the cardinalities, more severe the deviation.

References

[Lewis 2019] Jonathan Lewis. (2019, June 6). Scalar Subquery Costing

Thanks for sharing

Scalar Subqueries with OUTER JOIN

Cost calculation

Filling the cache

Cache misses

Outer join

Summary

Related blog posts

References

Nenad Noveljic

Leave a Reply Cancel reply